개념정리문제
- optical flow를 적용하기 위한 가장 중요한 가정(전제)은?
- optical flow equation과 각 항들이 의미하는바는?
- Lucas-Kanade 기법을 쓰는 이유
- Lucas-Kanade의 단점을 보완하기 위한 방법은?
위 질문에 답하지 못한다면 공부합시다.
optical flow(광류)를 적용하기 위해서는 한가지 가정이 필요하다. 바로 밝기 항상성인데, 이전 프레임과 현재프레임간의 밝기차이가 없거나 매우 작다는 가정이다.
이 가정하에 식을 하나 구할 수 있다.

여기서 우항을 정리하면
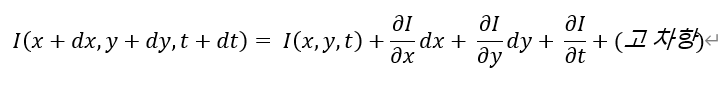
이 때, dt가 매우 작다는 가정하에 위의 두 수식을 이용하여 테일러근사를 적용하면 다음을 얻어낸다.

이 수식을 다시 정리하면

이 된다.
여기서

는 그레디언트로 한 프레임의 한 좌표만 있어도 구할 수 있다.
그레디언트는 한 픽셀에 대한 밝기변화방향이라고 할 수 있다.

이므로 한 좌표에 대해 현재프레임과 다음프레임만 있으면 구할수 있다.
따라서 이제 남은 미지수는 u,v인데 방정식이 하나이므로 미지수를 확정지을 수 없다.
따라서 optical flow equation을 풀기위해 Lucas-Kanade알고리즘과 Horn-schunk 알고리즘이 제안되었다.
Lucas-Kanade알고리즘은 지역전 연산을 다루고 Horn-schunk알고리즘은 전역적 알고리즘을 다루고 있는데 여기서는 Lucas-Kanade 알고리즘에 대해서 다뤄보기로 하겠다.
Lucas-Kanade 알고리즘은 optical flow equation이 한 방정식에 대해 미지수가 2개이므로 풀 수 없다는 것을 고려하여 같은 motion vector를 가지는 여러픽셀들을 다같이 고려하여 motion vector(u,v)를 구하는 방법이다.
5x5 윈도우를 생성하여 그 윈도우 안에 들어가는 물체에 대해서는 같은 방향으로 움직일 것이라고 가정한다.

이 때 motion vector를 의미하는 d는 다음과 같이 구한다.

이 때, Lucas-Kanade의 가정에 의하면 같은 motion vector를 가지는 작은 window에 대하여 적용하는 알고리즘이므로 만일 영상내의 object가 큰 움직임의 motion vector를 가진다면 aliasing 이 발생한다.

따라서 이 문제를 해결하기 위해 Pyramid방법이 제시된다.


정리하자면 왼쪽 초록색 피라미드는 과거 frame이고 오른쪽 파란 피라미드는 현재 frame이다. 피라미드의 가장 아랫단은 original frame size이고 위로 갈수록 1/2배 사이즈가 된다.
피라미드 method에 대해서 간단한 의사코드는 다음과 같다.
while(피라미드)
{
현재 층에서 now(u,v)를 구한다.
now(u,v) = now(u,v) + pre(u,v)
pre(u,v) = now(u,v)
피라미드 다음 층으로
}
while문을 나온 후 도출 된 now(u,v) 큰 motion vector에 대해서도 유효하다.