전체 개요 한눈에 보기

선형회귀 - 개념

가로축 : input, 세로축 : output
파란점 : 주어진 data.
회귀란 주어진 discrete한 데이터들을 한눈에 이해하기 쉽게 그래프로 근사하고자 하는 방법이다.
그런데 어떤 직선으로 회귀시켜야 데이터를 오차없이 가장 잘 근사시키는 건지 알아보자.
선형회귀 시키면 위 그림과 같이 여러개의 직선이 나온다.
이 때 회귀식은 다음과 같다.

선형회귀 - 개념 - error, residual, cost

이 때, 가장 잘 근사한 선형식은 당연히 error가 가장 작을 것이다.

residual : 선형회귀식과 data간의 차이를 말한다.
가장 왼쪽 점의 좌표를 x1,y1이라고 하자.
이 때 회귀식을 H(x) = wx + b 라고 하면, 회귀식이 x1일때 예측한 값은 wx1+b가 된다.
따라서 x1에 대한 residual은 y1 - (wx1 + b) 가 되고 이를 정리하면 y1 - H(x1)이다. (H(x1) - y1 이라고 해도 무방하다. )
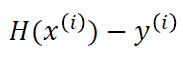
이 때 각각 데이터에 대한 error를 제곱해서 일반식으로 나타내면 다음과 같다.

갑자기 1/2 가 어디서 나왔냐고 할 수 있는데 이건 나중에 이 식을 미분했을때 편하게 계산하기 위해 단순히 붙여준 가중치라고 생각하면 된다. 별 의미 없다.
따라서 회귀식에 대한 전체 error 비용을 식으로 나타내면

이 때 error의 전체 비용을 cost라고 한다.
정리하자면 선형회귀는 결국 cost를 최소화 하는 w,b를 찾는 과정 이는 곧 그래프(식)을 찾는 과정이 되고 이를 다른 말로 최적화라고도 한다.
cost를 최소화 하는 w,b를 어떻게 찾을 수 있을까??

위의 예제를 이용하여 w,b를 하나하나씩 대입해서 찾아보면 cost가 최소가 되는 w,b를 찾을 수 있다. 그러나 이 방법은 당연히 효율적이지 못하다.
언제 효율적이지 못한가? 바로 input 데이터의 차원이 고차원으로 감에 따라 구해야 하는 w가 많아지기 때문이다.
==> w1,w2,w3,.... wn
만약 data input으로 들어갈 x가 x1,x2,x3로 3개씩 있다면 어떻게 될까?
H(x) = w1x1 + w2x2 + w3x3 + b 가 될것이다.
다시 정리하면 다음과 같다.

이 때 차원이 늘어남에 따라 효율적으로 w와 b를 찾는 방법이 필요하다.
이에 따라 효율적으로 w,b를 찾는 방법론이 제안되는데 대표적인 두가지가 바로
direct soultion 법과 gradient descent법이다.
선형회귀 - 방법론 - direct solution
쉽게말하면 선형회귀식을 편미분을 통해서 w,b를 찾는 방법이다. 어째서 미분을 통해서 찾을 수 있다고 할 수 있을까??
그 이유는 다음과 같다.
input 데이터가 많아서 cost그래프가 고차원적인 양상을 띈다고 생각해보자

이 때 cost가 최소인 점은 당연히 극소값일 때고 다시말하면 미분해서 값이 0일때이다.
따라서 cost식을 미분하여 값이 0 이 나오게 하는 w,b를 찾는 것이다.

선형회귀 - 방법론 - Gradient descent
direct solution과는 다른 방법론이 하나 제시되는데 바로 경사하강법이다.
개념을 쉽게 이해해보자

cost그래프 위에서 구슬을 굴린다고 가정해보자. 구슬은 경사를 따라서 가장 아래까지 내려갈 것이다. 경사하강법도 마찬가지로 극소값을 찾는 방법이다.
만약 구슬이 놓인 곳의 기울기가 양수라면 구슬은 왼쪽으로 갈것이고, 구슬이 놓인 곳의 기울기가 음수라면 구슬은 오른쪽으로 갈것이다. 또한 기울기가 가파를수록 구슬은 아래로 많이 움직여야하고 기울기가 완만할 수록 구슬은 아래로 조금만 움직여야 한다.
이런 방식으로 cost그래프의 극소값을 찾자는 방법이다.

이 때, 문제가 되는 것은 좌, 우로갈때 한번에 얼마만큼씩 움직여야 극소값을 잘 찾을수 있냐에 대한 것이다.

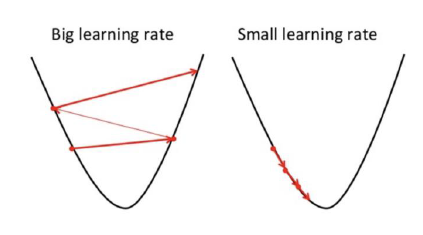
학습률이 클때 :
- 수렴한다면 학습속도가 빠를것이다. 큰 폭으로 극소값에 다가가기 때문이다.
- 너무 크면 구슬이 수렴하지 못하고 오히려 그래프 위로 튕겨져 나온다.
학습률이 작을때 :
- 발산할 위험이 적다.
- cost그래프의 극소값에 다가가는 속도가 느리다.
- 국소최적해에 머무를 가능성이 있다.
학습률이 너무 크거나 너무 작으면 둘다 문제가 있어 학습률을 택하는 방법도 제시된다. 그러나 이 부분에 대해서는 여기서 다루지 않겠다.
과연 direct solution법과 경사하강법중에 뭐가 더 좋을까?
답은 경사하강법이다.
direct solution은 정답을 명확하게 찾을 수 있다는 장점이 있지만, 데이터의 차원이 복잡해짐에 따라 계산해야하는 식이 너무 복잡해진다.
찾아야하는 w1,w2,w3, .... wn 이 있을 때, n이 너무 커진다는 말이다.
선형대수의 관점에서 말하자면 행렬의 크기가 너무 커져서 역행렬을 구하는데 필요한 연산량이 압도적으로 높아지게된다.
그러나 경사하강법은 고차원적인 경우에 대해서도 접근과 모델 설계가 쉽다는 장점이 있다.
이 장점때문에 경사하강법이 많은 모델에 대해서 적용되고 있다.
'공부공간 > Deep Learning' 카테고리의 다른 글
| [activation function] 활성화 함수를 쓰는 이유 (0) | 2020.05.20 |
|---|---|
| [딥러닝 강의정리] logistic regression (0) | 2020.04.09 |
| [딥러닝 강의 정리] linear classification (0) | 2020.04.07 |
| [딥러닝 강의정리] 2_Machine Learning Basics (0) | 2020.03.26 |
| [딥러닝 정리] 개념정리, 딥러닝의 활용 (0) | 2020.03.23 |