GAN관련 논문들을 읽다보면 항상 나오는 수식이 있다. 다음과 같이 E와 함께 쓰인 식인데 우선 살펴보도록 하자.

논문에서 직접 말하겠지만 참고로 (1)번 수식은 loss function이 아닌 objective function이다.
손실함수와 목적함수는 비슷하지만 분명히 다른데, 손실함수가 목적함수의 특별한 케이스라고 보면 된다.
간단하게 설명하자면 손실함수는 무조건 작을 수록 좋은것이지만 목적함수는 최소화를 목표로 할 수 도있고, 최대화를 목표로 할 수도 있다. 그러나 마찬가지로 목적함수로 학습의 최적화를 위해서 존재하는 함수라는 점에서 loss function과 비슷한 부분이 있다.
다시 논문내용으로 돌아가서 (1)은 loss function이 아니기 때문에 log(D(x,y))와 log(1-D(x,G(x,z)))가 최소가 아니라는 점에서 불편해 할 필요 없다.
오히려 loss function은 그 밑에 나오는 다음 문장이 loss라고 볼 수 있다.
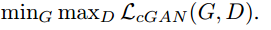
이 문장을 읽어보자.
"LcGAN을 최대로 하길 원하는 D와 그값을 최소로 하길 원하는 G" 라고 읽으면 된다.
즉, minmax(objective)는 최댓값을 최소로 하게 하는 function이다. 반대로 maxmin(objective)는 최소값을 최대로 하게 하는 function이 된다. 최댓값을 최소로하게 하는 function이면 함수 모양이 어떻든 간에 함수를 대체로 작아지게 하는 모양이 될것이다. 그래서 minmaxLcGAN 이 loss function이라고 한 것이다.
마지막으로 저 수식에서 불편한점 한 가지를 더 짚고 넘어가자. 바로 Exy.
확률통계 고수는 E를 보고 불편해 하지 않겠지만 나 같은 수학 초보자는 저런 수식을 보면 굉장히 마음이 불편하다. 이 참에 확실히 알고 넘어가도록 하자.
E는 기댓값을 말한다. 기댓값이란 어떤 확률분포에서 sampling했을 때 이 값이 나올것이다 라고 가장 기대할 수 있는 값을 말한다.
즉 첫번째 수식은 다음과 같이 읽으면 된다.
L = E(A) + E(B)
A라는 확률분포에서 a가 나올거고 B라는 확률분포에서 b가 나올건데 그 값을 합친게 목적함수가 된다.
근데 D는 a+b가 최대가 되길 원하고, G는 a+b가 최소가 되길 바라네.
즉, (1)번 식에서 D는 y가 들어올 때 1, G(x,z)가 들어올 때 0이 되길 바라지만
G는 목적함수가 최소가 되길 바라니까 log(1-D(x,G(x,z)))가 최대한 작아지길 바라겠네. 다시말해서 D(x,G(x,z))가 1이 되길 바라겠네. 즉, D의 output이 1이 되길 바란다는건 G는 D를 속여서 real로 인식하기를 바란다는 거구나.
라고 읽으면 된다.
참고 사이트 :
'연구 > papers' 카테고리의 다른 글
| [논문 리뷰] End-to-end object detection with transformers 빠르게 이해하기(DETR 리뷰) (2) | 2021.05.10 |
|---|---|
| [논문정리] (AlexNet) ImageNet Classification with Deep ConvolutionalNeural Networks (0) | 2020.10.01 |
| [ResNet] resenet이 degradation에 robust한 이유 고찰 (0) | 2020.09.09 |
| [논문 정리] Pose Machines: Articulated Pose Estimation via Inference Machines (0) | 2020.04.04 |
| [CPM 논문 정리] Convolutional Pose Machines (0) | 2020.04.03 |



